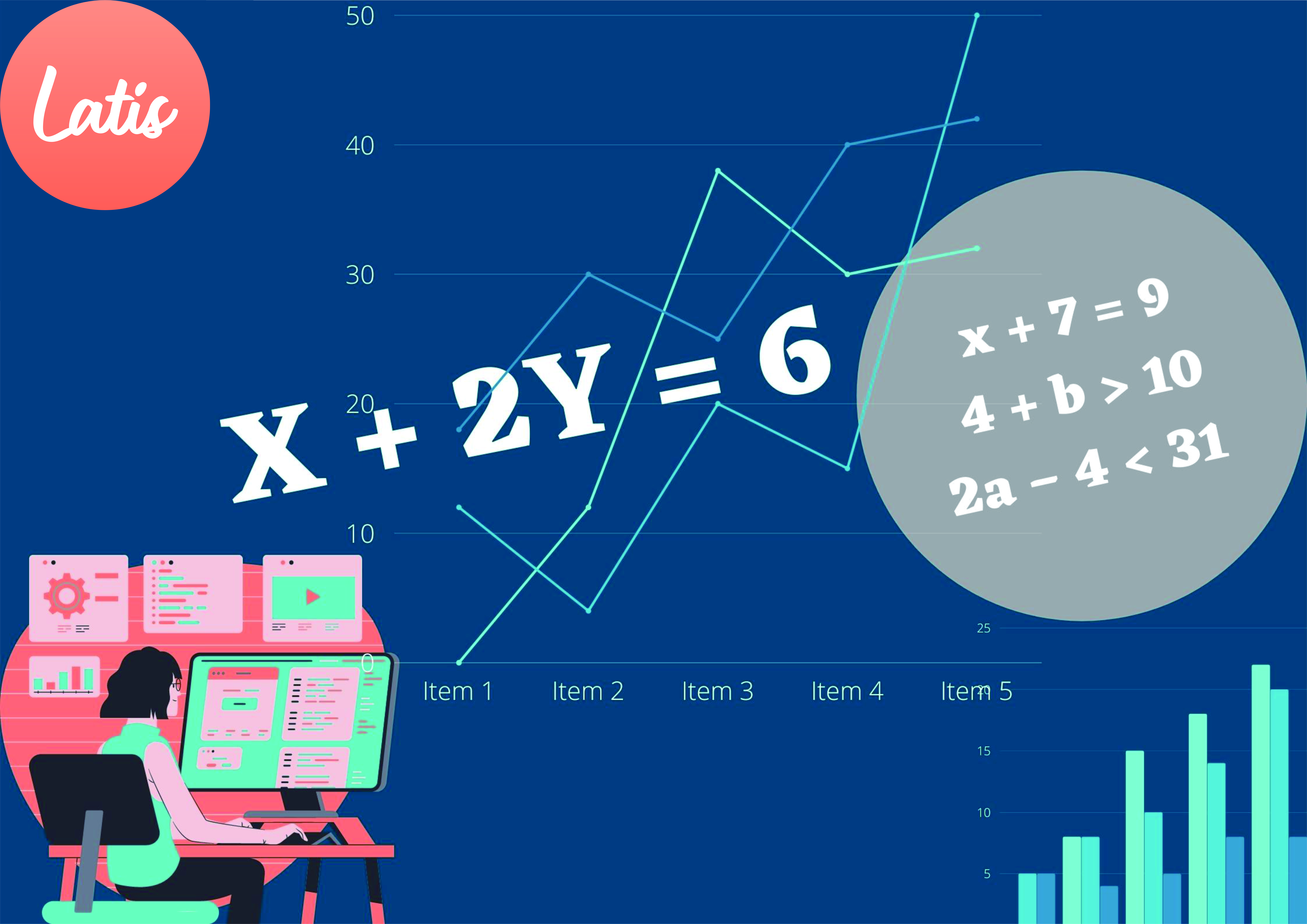Persamaan dan Pertidaksamaan Linier Satu Variabel │Matematika Kelas 7

Apa kamu pernah memperhatikan benda-benda di lingkungan sekitar yang berkaitan dengan persamaan dan pertidaksamaan linier? Sebagai contoh, sebuah truk seberat 15.000 kg (tanpa muatan) mengangkut 9 mobil sedan baru dengan jenis yang sama untuk dikirim ke dealer. Ketika beratnya diukur pada jembatan timbang, ternyata truk beserta muatannya memiliki berat 28.050 kg. Dapatkah kamu mengetahui berat mobil per unit? Dengan membentuk model matematika: 9x + 15.000 = 28.050 (persamaan linier satu variabel) dan menyelesaikannya, kamu akan mendapatkan jawabannya.

A.   Kalimat Tertutup dan Kalimat Terbuka

Sebuah kalimat dapat dibuat dengan kata-kata biasa atau dengan menggunakan lambang-lambang tertentu. Dalam matematika, sebuah kalimat dapat dikategorikan ke dalam dua bagian besar, yaitu kalimat tertutup dan kalimat terbuka.

           1.    Kalimat Tertutup (Pernyataan)

Perhatikan kalimat-kalimat berikut:

a.    6 + 4 = 10

b.    9 adalah bilangan genap

c.    Jika x bilangan asli maka 2x dan 2 bilangan ganjil

Dari ketiga kalimat di atas terlihat bahwa ruang lingkup pembahasan hanya ada dua kemungkinan, yaitu benar atau salah. Dengan rincian, kalimat (a) menyatakan kalimat yang benar karena memberikan informasi yang sesuai dengan keadaan yang ada. Kalimat (b) dan (c) menyatakan kalimat yang salah karena informasi yang diberikan bertentangan dengan kenyataan yang ada. Kalimat benar atau salah disebut kalimat tertup atau pernyataan.

1)    Kalimat yang benar adalah kalimat yang menyatakan hal-hal yang sesuai dengan kenyataan/keadaan yang berlaku umum.

2)    Kalimat yang salah adalah kalimat yang menyatakan hal-hal yang tidak sesuai dengan kenyataan/keadaan yang berlaku umum.

3)    kalimat yang bernilai benar atau salah disebut kalimat tertutup atau sering disebut dengan pernyataan.

          2.    Kalimat Terbuka, Variabel, dan Konstanta

Kalimat terbuka adalah kalimat yang belum dapat ditentukan nilai kebenarannya, bernilai benar saja atau salah saja karena memiliki unsur yang belum diketahui nilainya.

Perhatikan contoh-contoh berikut:

a.    □ + 2 = 6

b.    2x – 3 = 7

c.    ∆ adalah bilangan ganjil yang kurang dari 5

Ketiga kalimat di atas belum dapat ditentukan sebagai kalimat benar atau salah karena masih bergantung pada unsur tertentu. Kalimat (a) bergantung pada □, kalimat (b) pada x, dan kalimat (c) pada ∆.

Kalimat-kalimat tersebut disebut dengan kalimat terbuka. Unsur tertentu dari masing-masing kalimat terbuka disebut pebuah atau variabel. Kalimat (a) akan menjadi kalimat tertutup jika □ diisi. Jika diisi 4 maka kalimat dikatakan benar dan jika diisi selain 4 maka kalimat dikatakan salah. Adapun pengganti dua variabel yang berupa bilangan disebut konstanta.

1)    Kalimat terbuka adalah kalimat yang belum diketahui nilai kebenarannya (benar atau salah).

2)    Variabel adalah lambang atau simbol yang dapat diganti oleh sembarang anggota dari himpunan semesta.

3)    Konstanta adalah pengganti dari suatu variabel.

Contoh 1:

a.    Dua dikurang m sama dengan satu. Merupakan kalimat terbuka karena memiliki variabel yaitu m.

b.    y adalah bilangan prima yang lebih dari empat. Merupakan kalimat terbuka yang memiliki variabel y.

c.    x + 7 = 9. Merupakan kalimat terbuka karena memiliki variabel x.

d.    4 + b > 10. Merupakan kalimat terbuka karena memiliki variabel b.

e.    2a – 4 < 31 Merupakan kalimat terbuka karena memiliki variabel a.

Suatu kalimat terbuka yang memiliki variabel harus diganti oleh satu atau lebih anggota dari himpunan semesta yang didefinisikan, sehingga kalimat terbuka yang diberikan akan menjadi benar. Pengganti variabel tersebut dinamakan selesaian. Himpunan semua selesaian dalam kalimat terbuka disebut himpunan selesaian.

Contoh 2:

a.    x + 2 = 6, pengganti x yang benar adalah 4. Jadi, selesaiannya adalah x = 4, dan himpunan selesaiannya adalah {4}.

b.    p adalah bilangan ganjil, p ∈ {1, 2, 3, ..., 10}. Pengganti p supaya pernyataan bernilai benar adalah 1, 3, 5, 7, dan 9. Jadi, himpunan selesaiannya adalah {1, 3, 5, 7, 9}.

c.    5x + 2 = 9, dengan x ∈ himpunan bilangan asli. Tidak ada pengganti x yang membuat pernyataan menjadi benar. Jadi, himpunan selesaiannya adalah ∅ atau { }.

B.   Menyelesaikan Persamaan Menggunakan Penjumlahan dan Pengurangan

Dalam menyelesaikan persamaan linear satu variabel, tujuannya adalah menyederhanakan persamaan untuk menyisakan variabel saja di salah satu sisi. Setiap langkah yang digunakan untuk menyederhanakan persamaan menghasilkan persamaan ekuivalen. Apakah yang dimaksud dengan persamaan ekuivalen?

Perhatikan persamaan-persamaan berikut.

1.    x + 1 = 3

2.    x + 2 = 4

3.    2x − 2 = 6

Bagaimanakah himpunan selesaian dari ketiga persamaan di atas? Ketiga persamaan tersebut memiliki himpunan selesaian yang sama. Persamaanpersamaan di atas disebut dengan persamaan yang ekuivalen atau persamaan yang setara. Persamaan yang ekuivalen dapat dimodelkan sebagai timbangan yang seimbang kemudian kedua lengan ditambah atau dikurangi oleh beban yang sama, tetapi timbangan masih dalam keadaan seimbang. Untuk memahami bagaimana persamaan yang ekuivalen digunakan untuk menentukan himpunan selesaian suatu persamaan.

C.   Menyelesaikan Persamaan Menggunakan Perkalian dan Pembagian

Pada kegiatan sebelumnya kalian telah menerapkan operasi penjumlahan dan pengurangan pada persamaan yang ekuivalen untuk menyelesaikan suatu persamaan. Pada kegiatan ini akan diperluas lagi dengan menggunakan operasi perkalian dan pembagian untuk menyelesaikan persamaan.

Contoh masalah:

Tentukan himpunan selesaian dari setiap persamaan linear dua variabel:

3x + 1 = −7

Penyelesaian:

3x + 1 = –7

3x + 1 – 1 = –7 – 1

3x = –8

3x/3 = -8/3

x = -8/3

            Himpunan selesaian dari persamaan 3x + 1 = –7 adalah {-8/3}

Referensi:

As'ari A.R, Tohir M, Valentino E, Imron Z, Taufiq I. (2017). Matematika SMP/MTs Kelas VII Semester I. Pusat Kurikulum dan Perbukuan, Balitbang, Kemendikbud

Simangunson, Wilson dan Sukino. (2006). Matematika untuk SMP Kelas VII. Jakarta: Erlangga.